Michel Thizon published in 2024 a paper explaining why earth’s always variable climate is constrained within a narrow range. Influence of Adiabatic Gravitational Compression of Atmospheric Mass on the Temperature of the Troposphere. Excerpts in italics with my bolds and added images
ABSTRACT
The temperature that the Earth’s surface would have without the greenhouse effect, with an atmosphere completely transparent to infrared radiation, or even without an atmosphere at all, is generally estimated at -18°C. The greenhouse effect is estimated to induce a warming of 33°C to justify the surface temperature of +15°C.
To explain this discrepancy, we examine, with the ideal gas law, to which the Earth’s atmosphere obeys with its normal conditions of pressure and temperature, the role that the adiabatic compression of the atmospheric mass subjected to gravity can play. The dimensional analysis of the ideal gas law demonstrates that compression of the atmosphere produces energy, which can be calculated in Joules.
The temperature of the atmosphere near the Earth’s surface is influenced by
its invariable atmospheric mass, solar irradiation and the greenhouse effect.
This calls into question the commonly established Earth’s energy budgets which consider almost exclusively radiative effects, and which deduce a back radiation attributed to the greenhouse effect which is abnormally high.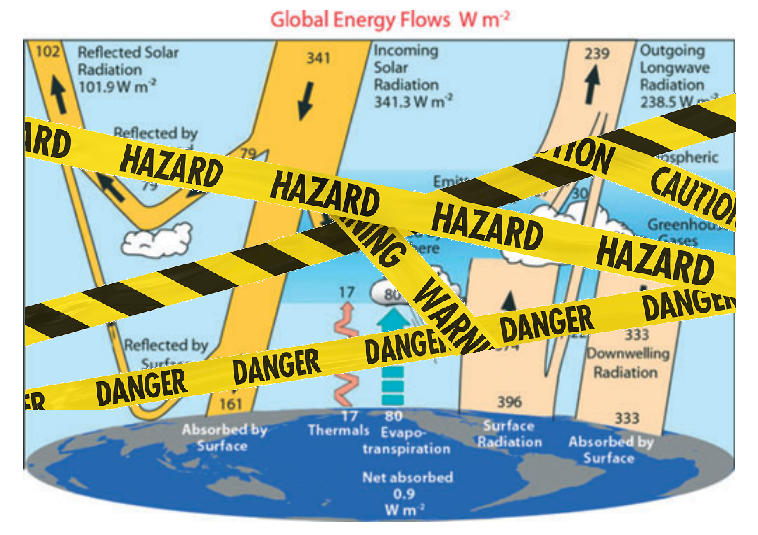
Earth temperature without atmosphere or greenhouse effects
Goody et al., estimated the solar energy available to heat, both directly and indirectly, the earth and its atmosphere at an average of 224 W/m-2 [1]. Applying the Stefan-Boltzmann law they assumed that the Earth radiates as a perfect black body in the infrared band at a temperature of 255.5 K (or min 17.6°C) for the effective emission temperature [2]. These authors noted that this temperature is lower than the average temperature of the Earth’s surface and indicated that much of the radiation to space must come from the atmosphere rather than from the surface. Goody et al., arbitrarily assigned a value of 1 to the emissivity ε for the calculation, while Jacquemoud assigned a value of 0.98 [3].
According to Hansen, a solar irradiance of 1367 W/m-2 or generally accepted today 1361 W/m-2, but varying with solar fluctuations, leads to a surface temperature of 255 K (or min 18°C), which induces a greenhouse effect of +33°C [4] Cotton reported that the emission temperature is -19°C and the earth temperature is +14°C, which corresponds to a global greenhouse effect of +33°C [5]. The global greenhouse effect is also estimated at +33°C [6-8]
.
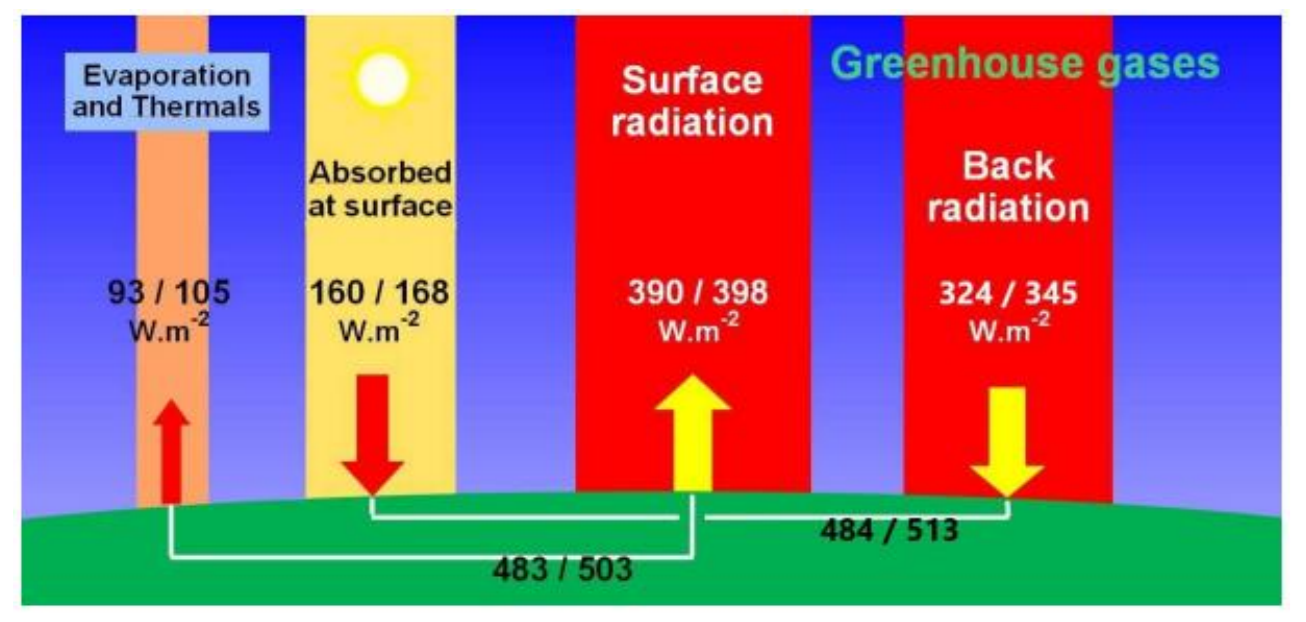
Logically, at -18°C the surface of the earth without an atmosphere or with an atmosphere totally transparent to longwave radiation and that plays no physical role, without any greenhouse effect, should be entirely frozen and covered with frost over its entire surface. This would result in a high Albedo which could be on the order of 0.5 to 0.9 instead of an albedo of 0.30 or 0.29 generally accepted in its current state. In this situation, instead of the solar energy absorbed by the surface reaching approximately 160 to 168 W/m-2 (Figure 1) this energy could be on the order of 70 W/m-2 [9-11]. The Stefan-Boltzmann formula yields a potential surface temperature of approximately -85°C [2]. Note that at these temperatures the water vapor pressure above ice is infinitesimal and could only generate an infinitesimal greenhouse effect. However, according to Nikolov et al., the effects linked to the atmosphere would bring approximately 90°C and not 33°C to the surface at a temperature of 15°C [12,13]. This would suggest that the global natural effect of atmosphere could be on the order of 90°C rather than the 33°C of the traditional purely radiative approach as reported by almost all the authors.
Global mean energy budget of the Earth
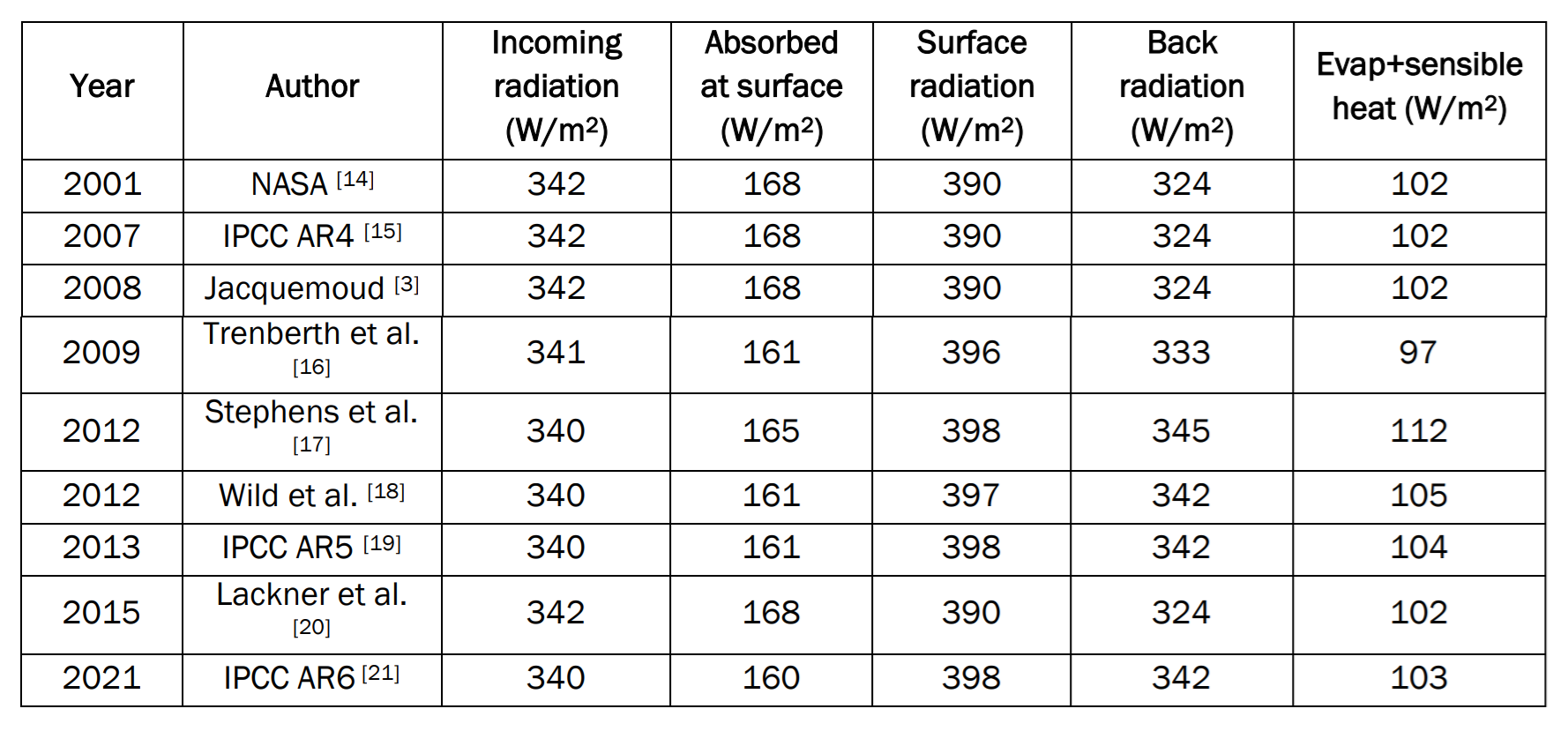
Many authors have endeavored to establish an overall assessment of the energy flows to which the earth is subjected to justify the surface temperature in an essentially radiative system. The Intergovernmental Panel on Climate Change (IPCC) itself places great emphasis on this in each of its reports. The Figure 1 summarizes the values and differences obtained while Table 1 summarizes the main authors who evaluated this earth assessment over a period of approximatively twenty years.
The dispersion and imprecision of the results do not allow the effect on surface temperature to be deduced with sufficient accuracy. These budgets must be improved as noted by Lupo et al. [22]
Effect of atmospheric pressure
Few authors have mentioned the role that an atmospheric mass subject to gravity could play in temperature. We can nevertheless cite Leroux [23] Jelbring [24], and Chilingar [25] but these authors evoke a potential role of atmospheric pressure on a qualitative level without seeking to calculate and quantify the effects, probably given the difficulty of integrating the atmosphere as a whole. Nikolov et al. clarify the role of atmospheric pressure for several planets through a complex semiempirical iterative approach [11]
Dimensional analysis of the ideal gas law PV=nRT
The ideal gas law PV=nRT is one of the most fundamental laws of physics and applies entirely to the lower troposphere under its usual conditions of pressure and temperature. This universally accepted law, established in 1834 by Émile Clapeyron, has been perfectly stable for nearly 200 years, which is the case for very few physical laws.
- P is the pressure (Pa);
- V is the volume of the gas (m3);
- n is the quantity of material (mol);
- T is the absolute temperature (K);
- R is the universal constant of ideal gases (8.314 J K−1 mol−1);
Dimensional analysis leads to:
R=PV/nT i.e., J K−1 mol−1=Pa.m3 K−1 mol−1, Hence J=Pa.m3=energy
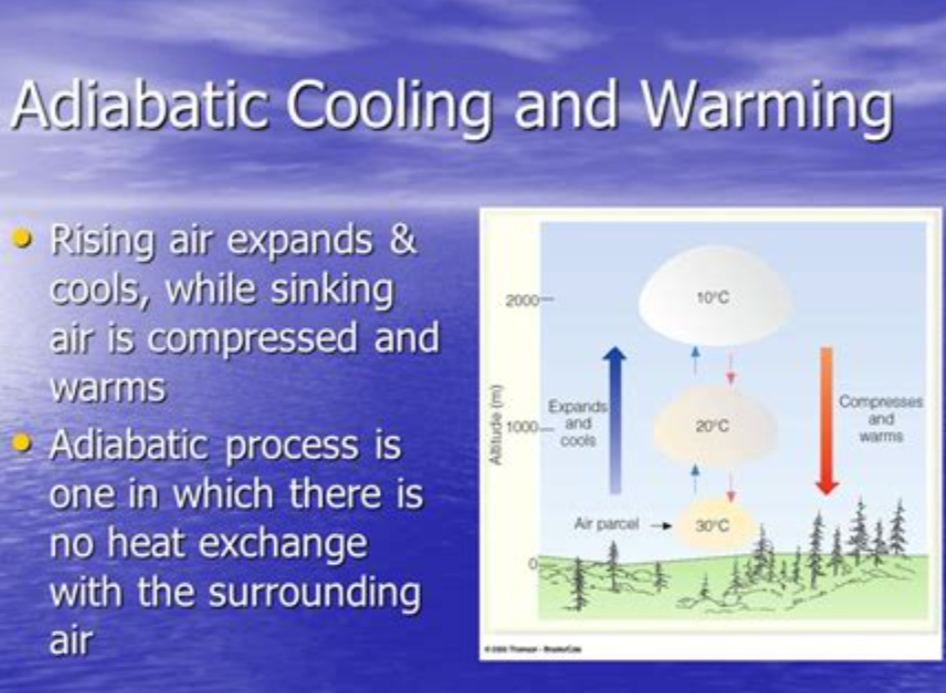
The volume of air multiplied by the pressure to which it is subjected is considered energy (Joules). The atmosphere is heated by compression due to the gravitational field to which it is subjected. Isolated in space, the Earth can only exchange energy with space by radiation, but the atmospheric mass cannot radiate spontaneously since its homonuclear constituents O2, N2, and Ar are passive and cannot radiate.
The earth’s surface is warmer and the atmosphere cannot cool down on contact with it. The compression is thus adiabatic. The greenhouse gases contained in the atmosphere at low levels, mainly H2O and CO2, are capable of radiating at long wavelengths but do not interact radiatively with O2 and N2; additionally, they are under the influence of permanent terrestrial infrared radiation, which they are capable of absorbing, and which is generated continuously from the solar energy received by the Earth’s surface.
The process includes the upward expansion, toward vacuum of the agitated molecules whose kinetic energy decreases and therefore the pressure, which causes cooling with altitude. It is not due to a decrease in gravity which decreases by less than 3/1000 at a 10 km altitude but of a struggle between gravity and the suction of the vacuum, until the equilibrium which defines an adiabatic thermal gradient. Gravity nevertheless prevents air molecules from escaping into space. Only some H2 molecules can reach the release speed.
RESULTS Heating of the atmosphere in °K by adiabatic compression
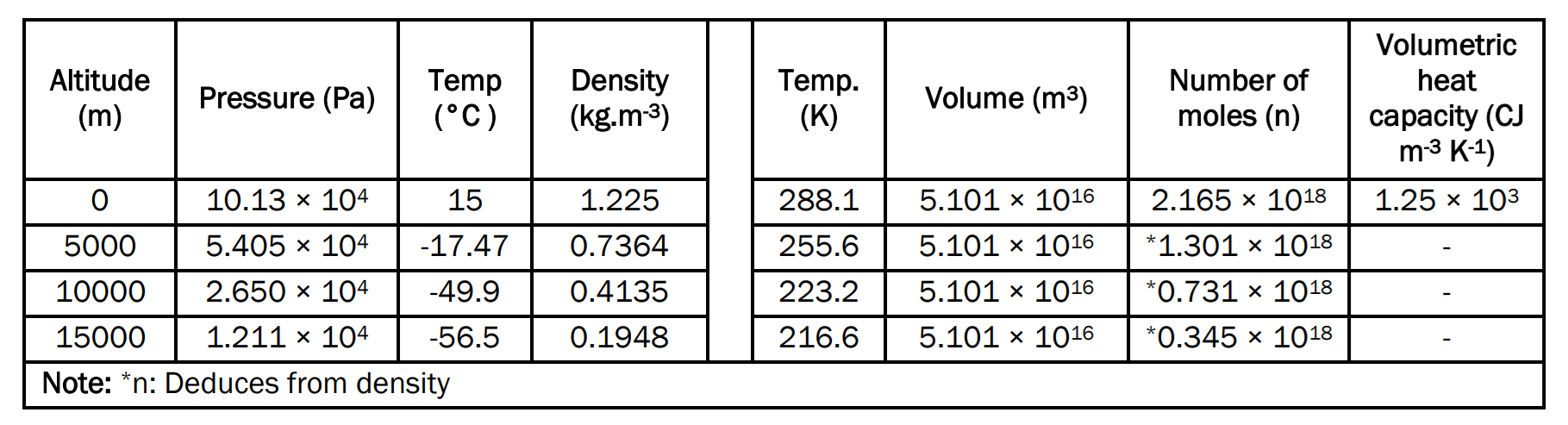
Table 2. Data for an air layer 100 m thick. The left part is from U.S. Standard Atmosphere, according to The EngineeringToolBox [26]
Altitude 0 m
- PV=(10.13 × 104 Pa) (5.101 × 1016 m3)=5.167 × 1021 J
- Volumetric heat capacity of air C=1256 J m−3 K−1 (at 0 m, 15°C)
- For 5.101 × 1016 m3 of air; +1°K requires 1256 × 5.101 × 1016 J=6.41 × 1019 J
- 5.167 × 1021 J/6.41 × 1019 J=80.7
- +80.7 K overheating due to pressure
Note: With an air layer of 200 m the precision is lower and leads to an overheating of 80.6 K
Gravity compression results, to the Earth’s surface, in 80.7°C of natural greenhouse energy equivalence, which means that to reach 15°C the initial temperature without atmosphere would be -65.7°C, very different from the -18°C admitted by radiative approaches for an inactive atmosphere.
Direct application of the ideal gas law T=PV/nR
- Altitude 0 m T=(10.13 × 104 × 5.10 × 1016)/(2.165 × 1018 × 8.314)=287.1 K (+14.0°C)
- Altitude 5,000 m T=254.9 K (-18.2°C)
- Altitude 10,000 m T=222.4 K (-50.7°C)
- Altitude 15,000 m T=215.3 K (-57.8°C)
The standard thermal gradient from 0 to 10 km is -6.49°C/km. The ideal gas law explains phenomena linked to temperatures up to 10,000 m in altitude. Beyond that, the results diverge, and other factors and phenomena are involved, like ozone and UV influence.
CONCLUSION
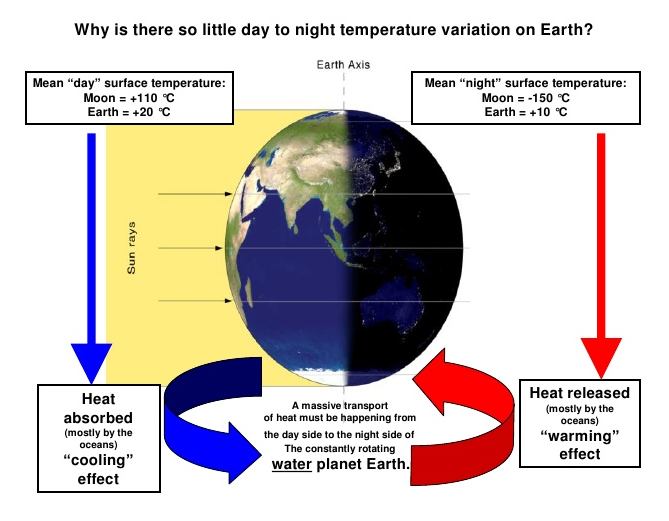
The temperature on the surface of the earth is mainly determined by the action of gravity on the atmospheric mass, which is an immutable fact on a scale of millennia. Climatic variations are the result of lesser phenomena. The solar influence is felt during the day by the direct radiation received, mainly when the sun is at its zenith, and the balance is modified by direct thermal exchanges between the sunny surface and the air in contact. The earth’s surface and the upper layers of the atmosphere radiate permanently towards space by emitting infrared radiation day and night, thus restoring the overall balance.
Surface infrared radiation is probably less intercepted in the lower troposphere by greenhouse molecules than is usually thought, thus explaining the surface temperature. However, there is an atmospheric dynamic, in particular through the water cycle, by evaporation-condensation, but whose overall energy balance is zero. Air mass movements and convection contribute to the overall dynamics, mainly due to the rotation of the Earth and the alternations between the presence and absence of solar radiation.
Astronomical fluctuations in sunshine, surface phenomena such as ocean currents, El Niño or La Niña phenomena, extreme weather phenomena or even volcanic eruptions, as well as other factors that are probably poorly characterized, lead to variations in surface temperature that nevertheless remain relatively damped due to the stabilizing effect of the invariable atmospheric mass subject to gravity.
See Also
Earth with no atmosphere and no oceans would be roughly the same average global surface temperature as the Moon, about -75°C.
Which can be calculated by using Stefan–Boltzmann for the sunlit side only, (divide by two not four) and averaging that with the mean dark side temperature:
394K * 0.5^0.25 = 331.3K
minus 12% albedo:
331.3K * 0.88^0.5 = 320.9K
averaged with a dark side T of 80K
(320.9 + 80) / 2 = 200.4k, which is within 2-3K of the DIVINER measurements.
Earth’s sunlit side at any given time is cooler than the sunlit surface of the Moon, because of clouds, water vapour absorbing solar near infrared, and Rayleigh scattering. But Earth’s average global surface temperature is much higher than the Moon, because of thermal reservoirs keeping Earth’s night side warmer. Mostly the oceans, then low clouds, and lastly water vapour.
CO2 has less heat capacity than dry air, the best it can do is boost daytime temperatures in hot dry regions.
LikeLike