A previous post elaborated a rigorous equation from Christos Vournas for calculating surface temperatures of planets or moons, for comparison with NASA satellite measurements of such bodies in our solar system. That post is How to Calculate Planetary Temperatures.
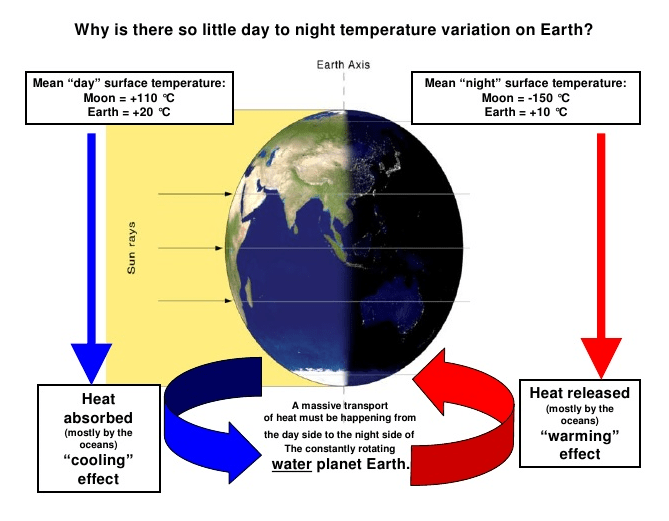
The image above presents the huge disparity in day and night temperatures between Earth and its Moon, and notes the role of ocean heat transport. But as I have learned from Christos, there is much more to the story, and this post discusses these deeper implications. He adds the rotational factor and its impact upon the radiation emitted by both bodies, ie. Earthshine and Moonshine (though obviously it is not simply visible light). Excerpts from Vournas are in italics with my bolds.

Moon and Earth – so close to each other – and so much different…
Moon is in our immediate neighborhood
Moon rotates around its axis at a slow rate of 29.5 days. The day on the Moon is 14.75 earth days long, and the night on the Moon is also 14.75 Earth days long.
Moon is in our immediate neighborhood. So Moon is at the same distance from the sun, as Earth, R=1 AU (astronomical unit). The year average solar irradiation intensity on the top of atmosphere for Moon and Earth is the same
So = 1361 W/m².
We say “on the top of the atmosphere”, it means the solar intensity which reaches a celestial body and then falls on it. For certain then, during these 14.75 earth days long lunar day the Moon’s surface gets warmed at much higher temperatures than the Earth.
There is the Planet Surface Rotational Warming Phenomenon
I’ll try here in few simple sentences explain the very essence of how the planet rotational warming Phenomenon occurs.
Lets consider two identical planets F and S at the same distance from the sun. Let’s assume the planet F spins on its axis Faster, and the planet S spins on its axis Slower. Both planets F and S get the same intensity solar flux on their sunlit hemispheres. Consequently both planets receive the same exact amount of solar radiative energy.
The slower rotating planet’s S sunlit hemisphere surface gets warmed at higher temperatures than the faster rotating planet’s F sunlit hemisphere. The surfaces emit at σT⁴ intensity – it is the Stefan-Boltzmann emission law.
Thus the planet S emits more intensively from the sunlit side than the planet F. There is more energy left for the planet F to accumulate then. That is what makes the faster rotating planet F on the average a warmer planet.
That is how the Planet Surface Rotational Warming Phenomenon occurs.
And it becomes very cold on the Moon at night
Moon gets baked hard during its 14,75 earth days long lunar day. And Moon also emits hard from its very hot daytime surface. What else can the very hot surface do but to emit hard, according to the Stefan-Boltzmann emission Law. The very hot surface emits in fourth power of its very high absolute temperature.
Jemit ~ T⁴
A warm object in space loses heat via emission. The hotter is the object, the faster it loses heat. So there is not much energy left to emit during the 14.75 earth days long lunar night.
The Table below shows the implications:
| Planet | Tsat mean | Rotations | Tmin | Tmax |
| Mercury | 340 K | 1/176 | 100K | 700K |
| Earth | 288 K | 1 | ||
| Moon | 220 Κ | 1/29.5 | 100K | 390K |
| Mars | 210 K | 0.9747 | 130K | 308K |
Comparing Mars and Mercury
The closest to the sun planet Mercury receives 15.47 times stronger solar irradiation intensity than the planet Mars does. However on the Mercury’s dark side Tmin.mercury = 100 K, when on the Mars’ dark side Tmin.mars = 130 K.
These are observations, these are from satellites the planets’ temperatures measurements. And they cannot be explained otherwise but by the planet Mars’ 171.5 times faster rotation than planet Mercury’s spin.
Earth-Moon temperatures comparison -why the differences
The faster (than Moon) Earth’s rotation smooths the average heat. The higher (than Moon) Earth’s surface specific heat capacity(oceanic waters vs dry regolith), also smooths the average heat. Consequently the daytime Earth’s surface temperature (compared to Moon) lessens, and the nighttime Earth’s surface temperature (compared to Moon) rises. Earth receives the same amount of solar heat (per unit area) from sun as Moon – for the same albedo. And Earth emits the same amount of solar heat, as the Moon does.
But something else very interesting happens.
It is the difference between Earth’s and Moon’s emitting temperatures. At the daytime Earth’s surface is warmed at a much lower temperatures and therefore at the daytime Earth’s surface emits IR radiation at a much lower intensities. So the intensity of Earth’s daytime IR radiation is much lower (than Moon’s).
As a result, there is a great amount of energy – compared to Moon – “saved” on Earth during the daytime emission.. This “saved” energy should be emitted by Earth’s surface during the nighttime then. At the night-time Earth’s surface is warmer than Moon’s and therefore Earth’s surface at night-time is at a higher temperatures. So the intensity of Earth’s night-time IR radiation is higher.
There is always a balance. The energy in = the energy out
But again something else very interesting happens.
In order to achieve that balance Earth’s night-time IR emitting intensity should be much higher than the night-time IR emitting intensity of the Moon. Now we should take notice of the nonlinearity of the Stefan-Boltzmann emission law. Consequently the night-time temperatures on Earth rise higher (compared to Moon) than the daytime temperatures on Earth lessens.
So the average Earth’s surface temperature is warmer (compared to the Moon). Thus Earth’s Tmean.earth = 288 K and Moon’s Tmean.moon = 220 K
The faster rotation and the higher specific heat capacity does not make sun to put more energy in the Earth’s surface. What the faster rotation and the higher specific heat capacity do is to modify the way Earth’s surface emits, the same amount as Moon, of energy (per unit area).
Earth emits IR radiation at lower temperatures during the daytime and at higher temperatures at night-time. Because of the nonlinearity of this process according to the Stefan-Boltzmann emission law, Earth ends up to have on average warmer surface than Moon.
The night-time temperatures on Earth rise higher (compared to Moon) than the day-time temperatures on Earth lessens. Earth receives (for the same albedo and per unit area) the same amount of solar energy as the Moon . This energy is “welcomed” on each planet and processed in a unique way for each planet.
To illustrate the above conclusions I’ll try to demonstrate on the Earth-Moon temperatures comparison rough example:
Surface temperatures
.min……mean……max
Tmin↑↑→T↑mean ←T↓max
Moon…100 K…220 K …390 K
Δ………..+84 K +68 K….- 60 Κ
Earth…184K↑↑.288 K↑.330 K↓
So we shall have for the faster rotating Earth, compared to the Moon:
Tmin↑↑→ T↑mean ← T↓max
+84↑↑→ +68↑mean ← -60↓
The faster a planet rotates (n2>n1) the higher is the planet’s average (mean) temperature T↑mean.
Note: To emphasize we should mention that Moon’s max and min temperatures are measured on Moon’s equator, and Earth’s max and min temperatures are not. Earth’s max and min temperatures are measured on continents, and not on oceanic waters. Otherwise the Δmin would have been even bigger and the Δmax would have been much smaller.
This rough example nevertheless illustrates that for the faster rotating and covered with water (higher cp) Earth compared with Moon the average temperature should be higher.
The planet’s faster rotation and the planet’s higher specific heat capacity “cp” not only smooths, but also processes ( Δmin > Δmax ), the same incoming solar heat, but in a different emission pattern.
Earth is warmer because Earth rotates faster and because Earth’s surface is covered with water
We had to answer these two questions:
1. Why Earth’s atmosphere doesn’t affect the Global Warming?
It is proven now by the Planet’s Mean Surface Temperature Equation calculations. There aren’t any atmospheric factors in the Equation. Nevertheless the Equation produces very reasonable results:
Tmean.earth = 287,74 K, calculated by the Equation, which is the same as the Tsat.mean.earth = 288 K, measured by satellites.
Tmean.moon = 223,35 K, calculated by the Equation, which is almost identical with the Tsat.mean.moon = 220 K, measured by satellites.
2. What causes the Global Warming then?
The Global Warming is happening due to the orbital forcing.
And… what keeps Earth warm at Tmean.earth = 288 K, when Moon is at Tmean.moon = 220 K? Why Moon is on average 68 oC colder? It is very cold at night there and it is very hot during the day…
Earth is warmer because Earth rotates faster and because Earth’s surface is covered with water.
Does the Earth’s atmosphere act as a blanket that warms Earth’s surface?
No, it does not.
.
Reblogged this on Climate Collections.
LikeLike
Ron, yes, I like it very much. Ron, you have the rare ability… thank you very much!
And please continue…
Best regards,
Christos
https://www.cristos-vournas.com
LikeLike